三角不等式 - ぬうがくブログ

三角不等式について気になったので
調べたり考えたりしたことを備忘録的にまとめておきます。

三角不等式は，三角関数の項( $\sin,\cos,\tan$ など)が含まれる不等式のことではなく
ここでは次のような不等式を言います。

三角不等式

実数 $a,b$ について，次の不等式が成り立ちます。

$|a+b| \leqq |a|+|b|$

$a,b$ それぞれの絶対値の和は，必ず $a,b$ の和の絶対値以上になるというのが
この不等式の主張です。

$a,b$ が同符号のときは明らかに成り立ちそうですし(例: $|2+3| \leqq|2|+|3|$ )
異符号のときは右辺のほうが大きくなりそうです(例: $|-2+3| \leqq |-2|+|3|$ )。

"成り立ちそう"ではなくて，きちんと証明してみます。

【証明】三角不等式

絶対値の定義より， $|a+b| \geqq 0,|a| \geqq 0,|b| \geqq 0$ なので
$|a+b| \leqq |a|+|b|$ を示すのに $(左辺)^2 \leqq (右辺)^2$ を示してよいです。
\begin{align}
(右辺)^2 - (左辺)^2 &= (|a|+|b|)^2 -|a+b|^2\\
&=|a|^2+2|a| \cdot |b| +b^2 - (a+b)^2\\
&=a^2 +2|a| \cdot |b| +b^2 - (a^2+2ab+b^2)\\
&=2|ab| - 2ab\\
&=2(|ab| - ab)
\end{align}
ここで， $|ab| \geqq ab$ なので $2(|ab| - ab) \geqq 0$ がいえます。
なぜなら実数 $x$ の絶対値 $|x|$ について
$x \geqq 0$ のとき $|x|=x$
$x \leqq 0$ のとき $|x| = -x \geqq 0 \geqq x$ なので
これらをまとめて $|x| \geqq x$ がいえるからです。
(そして $x=ab$ とおけばよいです。)

したがって $|a+b| \leqq |a|+|b|$ が成り立ちます。

さて，三角不等式は「三角」と冠していますが，三角形の成立条件に関連しています。
図形的に理解するならば、ベクトルが有効です。

三角不等式(ベクトル)

ベクトル $\overrightarrow{a},\overrightarrow{b}$ について，次の不等式が成り立ちます。

$| \overrightarrow{a}+\overrightarrow{b} | \leqq | \overrightarrow{a}|+|\overrightarrow{b} |$

これは，次の図をもとに考えるとよいです。

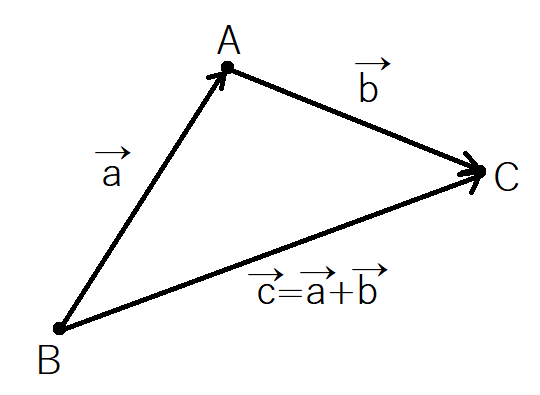
f:id:shibiremath:20210811215648p:plain

$|\overrightarrow{a}|$ は $\overrightarrow{a}$ の大きさであり，この図における線分ABの長さです。
件の不等式 $| \overrightarrow{a}+\overrightarrow{b} | \leqq | \overrightarrow{a}|+|\overrightarrow{b} |$ は
点Bから点Cへの直線距離(すなわち $|\overrightarrow{c}|=|\overrightarrow{a}+\overrightarrow{b}|$ )よりも
点Bから点Aを経由したのちに点Cへ行く道のり( $|\overrightarrow{a}|+|\overrightarrow{b}|$ )のほうが長くなる
という主張だとわかります。

ベクトルの場合も証明してみましょう。

【証明】三角不等式(ベクトル)

示すべき不等式は $| \overrightarrow{a}+\overrightarrow{b} | \leqq | \overrightarrow{a}|+|\overrightarrow{b} |$ です。

$\overrightarrow{a},\overrightarrow{b}$ の少なくとも一方が $\overrightarrow{0}$ のとき
例えば $\overrightarrow{b}=\overrightarrow{0}$ だとすると，
$|\overrightarrow{a}+\overrightarrow{b}|=|\overrightarrow{a}|$ であり， $|\overrightarrow{a}|+|\overrightarrow{b}|=|\overrightarrow{a}|$ なので不等式は成り立ちます。
同様にして $\overrightarrow{a}=\overrightarrow{0}$ の場合， $\overrightarrow{a}=\overrightarrow{b}=\overrightarrow{0}$ の場合も示すことができます。

よってそうでない場合の証明をします。

いずれも $\overrightarrow{0}$ でないベクトル $\overrightarrow{a},\overrightarrow{b}$ について
$| \overrightarrow{a} | \gt 0,| \overrightarrow{b}| \gt 0,| \overrightarrow{a}+\overrightarrow{b}| \gt 0$ なので
$| \overrightarrow{a}+\overrightarrow{b} | \leqq | \overrightarrow{a}|+|\overrightarrow{b} |$ を示すのに
$| \overrightarrow{a}+\overrightarrow{b} |^2 \leqq (| \overrightarrow{a}|+|\overrightarrow{b} |)^2$ を示してよいです。

\begin{align}
(右辺)^2 - (左辺)^2 &= (|\overrightarrow{a}+\overrightarrow{b}|)^2 - |\overrightarrow{a}+\overrightarrow{b}|^2\\
&= |\overrightarrow{a}|^2 + 2|\overrightarrow{a}| \cdot |\overrightarrow{b}| + |\overrightarrow{b}|^2 - (|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot \overrightarrow{b}+|\overrightarrow{b}|^2)\\
&=2(|\overrightarrow{a}|\cdot|\overrightarrow{b}|-\overrightarrow{a}\cdot \overrightarrow{b})
\end{align}
ここで，ベクトルの内積の定義 $\overrightarrow{a} \cdot \overrightarrow{b} = |\overrightarrow{a}| \cdot |\overrightarrow{b}| \cdot \cos \theta$ より
(ただし $\theta$ は $\overrightarrow{a},\overrightarrow{b}$ のなす角)
\begin{align}
2(|\overrightarrow{a}| \cdot |\overrightarrow{b}|-\overrightarrow{a}\cdot \overrightarrow{b})\\
=2(|\overrightarrow{a}| \cdot |\overrightarrow{b}|-|\overrightarrow{a}| \cdot |\overrightarrow{b}| \cdot \cos \theta)\\
=2|\overrightarrow{a}| \cdot |\overrightarrow{b}| (1- \cos \theta)\\
\end{align}
と変形できて， $-1 \leqq \cos \theta \leqq 1$ から $1- \cos \theta \geqq 0$ がいえるため
$2|\overrightarrow{a}| \cdot |\overrightarrow{b}| (1- \cos \theta) \geqq 0$ がわかります。

したがって， $| \overrightarrow{a}+\overrightarrow{b} | \leqq | \overrightarrow{a}|+|\overrightarrow{b} |$ が成り立ちます。

三角不等式は複素数においても成り立ちます。
それは次のとおりです。

三角不等式(複素数)

複素数 $z_1,z_2$ について，次の不等式が成り立ちます。

$|z_1+z_2| \leqq |z_1|+|z_2|$

複素数 $z=a+bi$ ( $a,b$ は実数， $i$ は虚数単位) をベクトル $(a,b)$ に対応させれば
二次元ベクトルに帰着できるので，確かに成り立つでしょう。
一応，証明してみます。

【証明】三角不等式(複素数)

示すべき不等式は $|z_1+z_2| \leqq |z_1|+|z_2|$ です。

複素数 $z_1=a+bi,z_2=c+di$ において，
$|z_1|=\sqrt{a^2+b^2} \geqq 0 , |z_2|=\sqrt{c^2+d^2} \geqq 0$
$|z_1+z_2|=\sqrt{(a+c)^2+(b+d)^2} \geqq 0$ なので
$|z_1+z_1|^2 \leqq (|z_1|+|z_2|)^2$ を示してよいです。

\begin{align}
&(右辺)^2-(左辺^2)\\
&=|z_1|^2+2|z_1| \cdot |z_2|+|z_2|^2 - \sqrt{(a+c)^2+(b+d)^2}^2\\
&=a^2+b^2+2|z_1| \cdot |z_2|+c^2+d^2-(a^2+b^2+c^2+d^2+2ac+2bd)\\
&=2\sqrt{(a^2+b^2)(c^2+d^2)}-2(ac+bd)
\end{align}
この値が0以上，つまり
$\sqrt{(a^2+b^2)(c^2+d^2)} \geqq (ac+bd) \tag{☆}$
がいえればよいです。

ここはちょっと困りましたが，シュワルツの不等式の力を借りようと思います。
シュワルツの不等式とは次のとおりです。

シュワルツの不等式

任意の正の整数 $n$ について，次の不等式が成り立ちます。

$\displaystyle\left(\sum_{i=1}^{n} x_i^2 \right) \left(\sum_{i=1}^{n} y_i^2 \right) \geqq \left( \sum_{i=1}^{n} x_i y_i \right)^2$

ただし，各 $x_i,y_i$ は任意の実数です。

このシュワルツの不等式において， $n=2$ とすると
$(x_1^2+x_2^2)(y_1^2+y_2^2) \geqq (x_1 y_1 + x_2 y_2)^2$ となり
これの両辺の平方根をとって， $x_1=a,x_2=b,y_1=c,y_2=d$ に対応させた姿が
まさに式(☆)になります。

そういうわけで，シュワルツの不等式より式(☆)は成り立ちます。

結局， $|z_1+z_2| \leqq |z_1|+|z_2|$ が成り立ちます。

シュワルツの不等式については，また別の機会に詳しく調べたいと思います。