単位円による三角関数の定義

本記事では単位円を使った三角関数の定義について紹介し
またそれをもとに，三角関数の性質について解説します。

よりわかりやすい解説を目指し
第1象限の角，第2，第3，第4象限の角，というように
それぞれの場合について考えていきます。

定義
第1象限の場合
第2象限の場合
第三象限の場合
第四象限の場合
特別な角の三角関数の値

定義

単位円による三角関数の定義

座標平面上に，原点 $O = (0,0)$ を中心とする半径 $1$ の円を描き
点 $A = (1,0)$ とします。
また円周上の任意の位置に点 $P$ をとり， $\angle POA = \theta$ とします。
このとき，点 $P$ の座標を， $P = (\cos \theta,\sin \theta)$ と表します。
また， $\cos \theta \neq 0$ の条件のもとで $\tan \theta = \displaystyle\frac{\sin \theta}{\cos \theta}$ とします。

このページでは，上の図を【定義の図】と呼ぶことにし
以降，この図をアレンジしながらたびたび扱います。

と言ってもこのままではわかりにくいかもしれません。
各象限に分けて，例を見てみましょう。

第1象限の場合

点 [texP] が第1象限にある場合から考えます。
このときの図は先に述べた【定義の図】と同様です。

では，例えば $\theta = \displaystyle\frac{\pi}{6} (=30^{\circ})$ のときを考えてみましょう。

まず【定義の図】において $\theta=\displaystyle\frac{\pi}{6}$ とした図をかきます。
図のいらない部分は省略しますね。

上の図の点 $H$ は，点 $P$ から $x$ 軸に向かって引いた垂線と $x$ 軸との交点です。
ですから $\angle PHO = \displaystyle\frac{\pi}{2} (= 90^{\circ})$ です。
$\triangle POH$ は，次の三角形 $ABC$ と相似ですね。

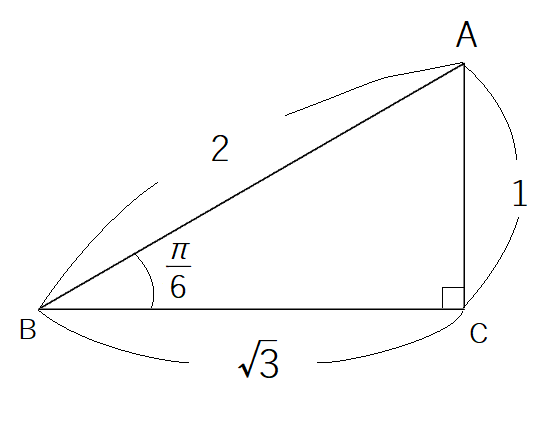
二つの図を比較して， $\triangle POH$ の各辺の長さを求めてみましょう。

【定義の図】において円の半径は $1$ としましたから， $PO = 1$ です。
$\triangle POH$ と $\triangle ABC$ は相似で，その相似比は辺 $PO$ と $AB$ の比から $1:2$ です。

したがって， $\triangle POH$ の辺の長さは次のようにわかります。

さて，【定義の図】の点 $P$ の座標を $(\cos \theta, \sin \theta)$ とするのでした。
この場合は $P=(\displaystyle\cos \frac{\pi}{6}, \sin \displaystyle\frac{\pi}{6})$ です。
点 $P$ の $x$ 座標は $OH$ ， $y$ 座標は $PH$ の長さそのものですね。

よって $\cos \displaystyle\frac{\pi}{6} = \frac{\sqrt{3}}{2}$ ， $\sin \displaystyle\frac{\pi}{6} = \frac{1}{2}$

さらに $\tan \displaystyle\frac{\pi}{6} = \frac{\sin \displaystyle\frac{\pi}{6}}{\cos \displaystyle\frac{\pi}{6}} = \displaystyle\frac{1}{\sqrt{3}}$ となります。

定義において円の半径を $1$ としていたのは
$OH , PH$ の長さがそのまま点 $P$ の $x$ 座標と $y$ 座標に対応してくれるからです。
また， $\tan \theta$ は直線 $OP$ の傾きに対応します。

例題1

(1) $\sin \displaystyle\frac{\pi}{4}$ ， $\cos \displaystyle\frac{\pi}{4}$ ， $\tan \displaystyle\frac{\pi}{4}$ の値をそれぞれ求めてください。

(2) $\sin \displaystyle\frac{\pi}{3}$ ， $\cos \displaystyle\frac{\pi}{3}$ ， $\tan \displaystyle\frac{\pi}{3}$ の値をそれぞれ求めてください。

例題1の解答

(1) $\sin \displaystyle\frac{\pi}{4} = \frac{1}{\sqrt{2}}$ ， $\cos \displaystyle\frac{\pi}{4} = \frac{1}{\sqrt{2}}$ ， $\tan \displaystyle\frac{\pi}{4} = 1$

(2) $\sin \displaystyle\frac{\pi}{3} = \frac{\sqrt{3}}{2}$ ， $\cos \displaystyle\frac{\pi}{3} = \frac{1}{2}$ ， $\tan \displaystyle\frac{\pi}{3} = \sqrt{3}$

第2象限の場合

例えば， $\theta = \displaystyle\frac{2 \pi}{3} (=120^{\circ})$ のときを考えてみましょう。
ここは $\displaystyle\frac{\pi}{3}$ をもとにして考えるとよいです。
【定義の図】をアレンジして次のような図をかきます。

点 $P$ ， $P'$ から $x$ 軸に向かって引いた垂線と $x$ 軸との交点をそれぞれ $H$ ， $H'$ とします。
この図において定義より，点 $P'$ の座標が $P'=(\cos \displaystyle\frac{2 \pi}{3},\sin \frac{2 \pi}{3})$ となりますから
これの具体的な値を求めることが目標です。

$\triangle POH$ と $\triangle P'OH'$ は合同です。
よって対応する辺の長さが等しく， $PH=P'H'$ ，また $OH=OH'$ となります。

辺 $P'H'$ の長さははまさに点 $P'$ の $y$ 座標で
それは点 $P$ の $y$ 座標，すなわち辺 $PH$ と等しいです。
点 $P'=(\cos \displaystyle\frac{2 \pi}{3},\sin \frac{2 \pi}{3})$

点 $P = ( \cos \displaystyle\frac{\pi}{3} , \sin \displaystyle\frac{\pi}{3})$ ですから

$P'H' = \sin \displaystyle\frac{2 \pi}{3} = \sin \displaystyle\frac{\pi}{3} = \frac{\sqrt{3}}{2}$
とわかります。

同様にして，辺 $OH'$ の長さは辺 $OH$ と等しいです。
ただし点 $H'$ の $x$ 座標，すなわち点 $P'$ の $x$ 座標は負であることに注意すると
$\cos \displaystyle\frac{2 \pi}{3} =- \cos \displaystyle\frac{\pi}{3} = - \frac{1}{2}$
となります。そして
$\tan \displaystyle\frac{2 \pi}{3} = \frac{\sin \displaystyle\frac{2 \pi}{3}}{\cos \displaystyle\frac{2 \pi}{3}} = - \sqrt{3}$
となります。

またこの考え方は， $\theta = \displaystyle\frac{\pi}{6}$ のときに限らず
次のように一般化できます。

図のように点 $P=(\cos \theta , \sin \theta)$ ， $P'=(\cos(\pi - \theta) , \sin (\pi - \theta))$ をとります。
点 $P$ と $P'$ の座標を比較すると，これらの $y$ 座標は等しいので

$\sin (\pi - \theta) = \sin \theta \tag{1}$
がいえます。同様に $x$ 座標を比較すると
$OH=OH'$ であることから符号が反転しているだけとわかるので

$\cos (\pi - \theta) = - \cos \theta \tag{2}$
がいえます。さらにこの(1)，(2)から

$\tan (\pi - \theta) = \displaystyle\frac{\sin (\pi - \theta)}{\cos (\pi - \theta)}=\displaystyle\frac{\sin \theta}{- \cos \theta} = - \tan \theta \tag{3}$
がいえます。
これは， $\theta$ がどのような実数値でも成り立ちます。

例題2

(1) $\sin \displaystyle\frac{3}{4} \pi$ ， $\cos \displaystyle\frac{3}{4} \pi$ ， $\tan \displaystyle\frac{3}{4} \pi$ の値をそれぞれ求めてください。

(2) $\sin \displaystyle\frac{5}{6} \pi$ ， $\cos \displaystyle\frac{5}{6} \pi$ ， $\tan \displaystyle\frac{5}{6} \pi$ の値をそれぞれ求めてください。

例題2の解答

(1) $\sin \displaystyle\frac{3}{4} \pi = \frac{1}{\sqrt{2}}$ ， $\cos \displaystyle\frac{3}{4} \pi = - \frac{1}{\sqrt{2}}$ ， $\tan \displaystyle\frac{3}{4} \pi = -1$

(2) $\sin \displaystyle\frac{5}{6} \pi = \frac{1}{2}$ ， $\cos \displaystyle\frac{5}{6} \pi = - \frac{\sqrt{3}}{2}$ ， $\tan \displaystyle\frac{5}{6} \pi = - \frac{1}{\sqrt{3}}$

第三象限の場合

ここからペースアップしていきましょう。

第三象限の角を考えるときは
第一象限の角 $\theta$ から $\pi (=180^{\circ})$ だけ回転させた角を考えるとよいです。

上の図のように点 $P=(\cos \theta , \sin \theta)$ ， $P'=(\cos ( \theta + \pi ) , \sin ( \theta + \pi ))$ をとります。
$\triangle POH$ と $\triangle P'OH'$ は合同です。
すると $PH = P'H'$ ですから，点 $P$ と $P'$ の $y$ 座標を比較すると
それらは符号が反転しているだけとわかるので

$\sin ( \theta + \pi) = - \sin \theta \tag{4}$
がいえます。

同様に $OH = OH'$ ですから，点 $P$ と $P'$ の $x$ 座標を比較すると
それらは符号が反転しているだけとわかるので

$\cos ( \theta + \pi) = - \cos \theta \tag{5}$
がいえます。そして(4)，(5)から

$\tan ( \theta + \pi) = \displaystyle\frac{\sin ( \theta + \pi)}{\cos ( \theta + \pi)} = \tan \theta \tag{6}$
がいえます。

これらは $\theta$ がどのような実数値でも成り立ちます。

三角関数のより具体的な値を考えるときは
式(4)，(5)，(6)を公式として適用するというよりは
図のほうを考えるとよいです。
たとえば $\sin \displaystyle\frac{7}{6} \pi (=210^{\circ})$ の値を求めるときは
$\theta = \displaystyle\frac{1}{6} \pi (=30^{\circ})$ とした図を描きます。

例題3

(1) $\sin \displaystyle\frac{7}{6} \pi$ ， $\cos \displaystyle\frac{7}{6} \pi$ ， $\tan \displaystyle\frac{7}{6} \pi$ の値をそれぞれ求めてください。

(2) $\sin \displaystyle\frac{5}{4} \pi$ ， $\cos \displaystyle\frac{5}{4} \pi$ ， $\tan \displaystyle\frac{5}{4} \pi$ の値をそれぞれ求めてください。

例題3の解答

(1) $\sin \displaystyle\frac{7}{6} \pi = - \frac{1}{2}$ ， $\cos \displaystyle\frac{7}{6} \pi = - \frac{\sqrt{3}}{2}$ ， $\tan \displaystyle\frac{7}{6} \pi = \frac{1}{\sqrt{3}}$

(2) $\sin \displaystyle\frac{5}{4} \pi = - \frac{1}{\sqrt{2}}$ ， $\cos \displaystyle\frac{5}{4} \pi = - \frac{1}{\sqrt{2}}$ ， $\tan \displaystyle\frac{5}{4} \pi = 1$

第四象限の場合

第四象限の角を考えるときは
第一象限の角 $\theta$ に対して $- \theta$ の角を考えるとよいです。

上の図のように点 $P=(\cos \theta , \sin \theta)$ ，[tex;P'=(\cos (- \theta) , \sin ( - \theta))] をとります。
$\triangle POH$ と $\triangle P'OH$ は合同です。
すると $PH=P'H$ ですから，点 $P$ と $P'$ の $y$ 座標を比較すると
それらは符号が反転しているだけとわかるので

$\sin (- \theta) = - \sin \theta \tag{7}$

がいえます。また点 $P$ と $P'$ の $x$ 座標は等しいので

$\cos (- \theta) = \cos \theta \tag{8}$

がいえます。そして(7)，(8)から

$\tan (- \theta) = \displaystyle\frac{\sin (- \theta)}{\cos (- \theta)} = - \tan \theta \tag{9}$

がいえます。

これら式(7)，(8)，(9)も， $\theta$ がどのような実数値でも成り立ちます。

またこの場合も，式(7)，(8)，(9)を公式として覚えて適用するよりは
図を考えることで，三角関数の具体的な値を求めるほうがよいです。
たとえば $\sin \displaystyle\frac{11}{6} \pi (=330^{\circ})$ の値を考えるときは
$\theta = \displaystyle\frac{1}{6} \pi (=30^{\circ})$ と $\theta = - \displaystyle\frac{1}{6} \pi (=-30^{\circ})$ をもとにした図を考えるとよいです。

例題4

(1) $\sin \displaystyle\frac{7}{4} \pi$ ， $\cos \displaystyle\frac{7}{4} \pi$ ， $\tan \displaystyle\frac{7}{4} \pi$ の値をそれぞれ求めてください。

(2) $\sin \displaystyle\frac{11}{6} \pi$ ， $\cos \displaystyle\frac{11}{6} \pi$ ， $\tan \displaystyle\frac{11}{6} \pi$ の値をそれぞれ求めてください。

例題4の解答

(1) $\sin \displaystyle\frac{7}{4} \pi = - \frac{1}{\sqrt{2}}$ ， $\cos \displaystyle\frac{7}{4} \pi = \frac{1}{\sqrt{2}}$ ， $\tan \displaystyle\frac{7}{4} \pi = -1$

(2) $\sin \displaystyle\frac{11}{6} \pi = - \frac{1}{2}$ ， $\cos \displaystyle\frac{11}{6} \pi = \frac{\sqrt{3}}{2}$ ， $\tan \displaystyle\frac{11}{6} \pi = - \frac{1}{\sqrt{3}}$

特別な角の三角関数の値

最後に $\displaystyle\frac{n \pi}{2}$ ( $n$ は整数) の角に対する三角関数の値を求めます。
要するに $90^{\circ}$ の倍数の角に対する三角関数の値です。
たとえば $\displaystyle\frac{\pi}{2}$ に対する三角関数の値は次のように考えます。

冒頭に述べた三角関数の定義を思い出してください。
原点を中心とする単位円周上の点 $P$ について
$\angle POA = \theta$ として点 $P=(\cos \theta , \sin \theta)$ とするのでした。
ならば次のような図を考えましょう。

点 $P$ の座標を考えてみてください。
点 $P$ は $y$ 軸上の点ですよね。さらに円の半径が $1$ であることに注意すると
$P = (\cos \displaystyle\frac{\pi}{2} , \sin \displaystyle\frac{\pi}{2}) = (0,1)$ です。
したがって
$\cos \displaystyle\frac{\pi}{2} = 0$ ， $\sin \displaystyle\frac{\pi}{2} = 1$ となります。

また $\tan \displaystyle\frac{\pi}{2}$ については
$\tan \displaystyle\frac{\pi}{2} = \displaystyle\frac{\sin \displaystyle\frac{\pi}{2}}{\cos \displaystyle\frac{\pi}{2}}$
で，分母の値が $0$ になってしまうため値を定義できません。
したがって $\tan \displaystyle\frac{\pi}{2}$ の値はありません。
( $\tan \displaystyle\frac{\pi}{2}$ の値は $0$ という意味ではありません)