三角関数の方程式1
本記事を読む前に,次の記事の内容を理解していると
スムーズに読み進められると思います。
本記事では,三角関数の方程式のうち
最も簡単なものについて解説します。
早速次の例題を考えてみましょう。
例題1
次の についての方程式を解いてください。ただし
とします。
\begin{align}
\sin \theta = \frac{1}{2}
\end{align}
問題を考えるときは,まず定義に従って
問題の意味を考えることが大事です。
原点を中心とする半径 の円周上の点
について
その 座標を
とするのでしたね。
つまりこの問題は
「そのような点 の
座標が
になるのは
角 がいくらのときでしょう?」
という意味だと考えることができます。
図で表すと,次のような角 を求めることになります。
ここで,角 の候補は
つあることに注意しましょう。
図の緑色をつけた角 と,赤色をつけた角
です。
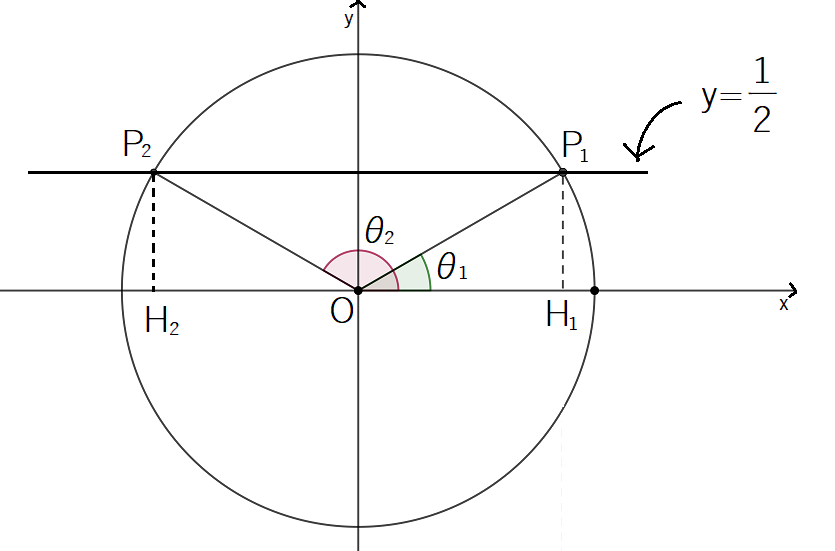
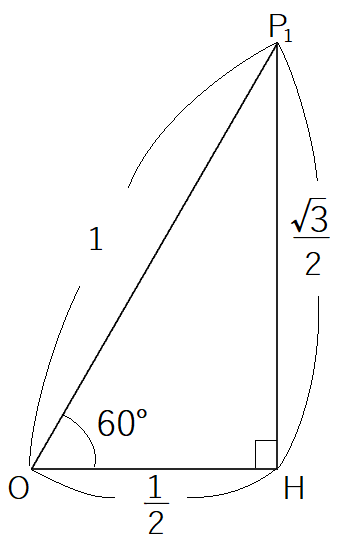
まず について考えます。
は次の図の
と相似です。
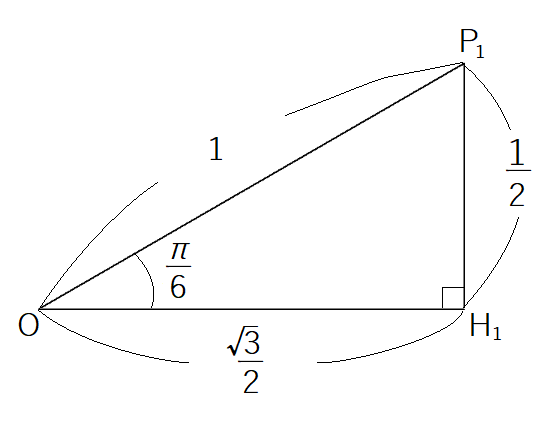
したがって角 は
とわかります。
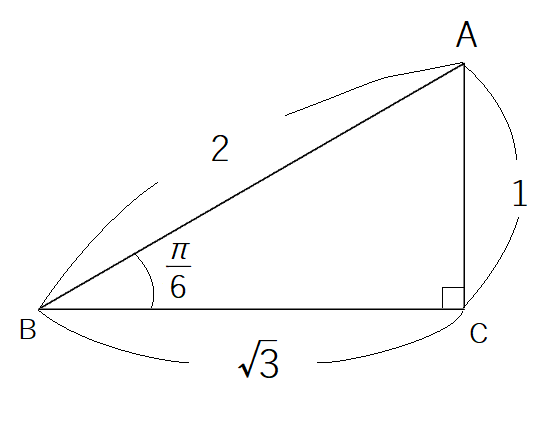
一方 については,
が先の
と相似ですから
となり,したがって
とわかります。
例題1の解答
では, の場合も解いてみましょう。
例題2
次の についての方程式を解いてください。ただし
とします。
\begin{align}
2 \cos \theta = 1
\end{align}
先ほどと同じように考えてみましょう。
おっと,その前に式の両辺を で割って
としておきましょう。
原点を中心とする半径 の円周上の点
について
その 座標を
とするのでした。
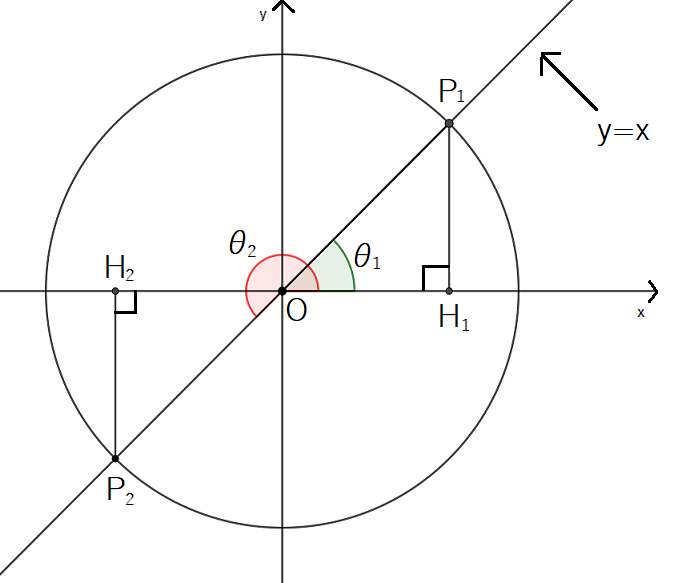
ということは,次の図のような位置の角 を求めることになります。
ここでも,候補が2つあることに注意しましょう。
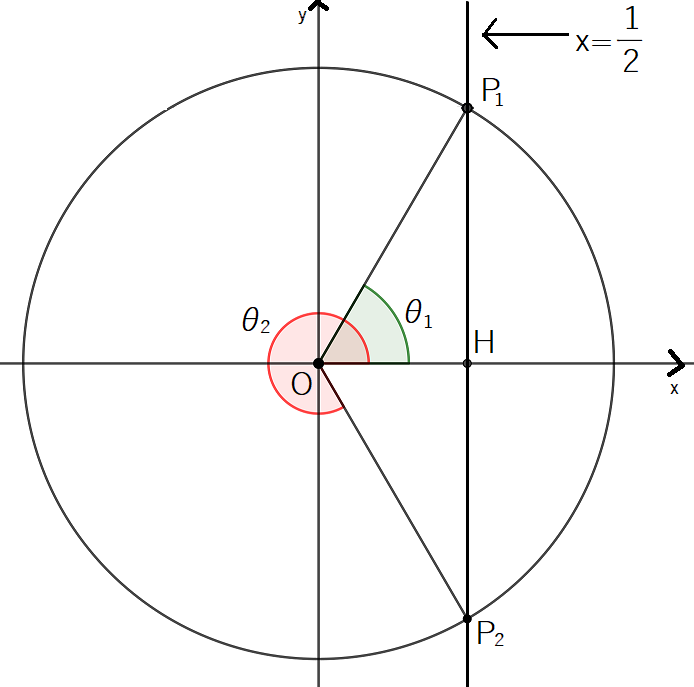
は次の
と相似です。
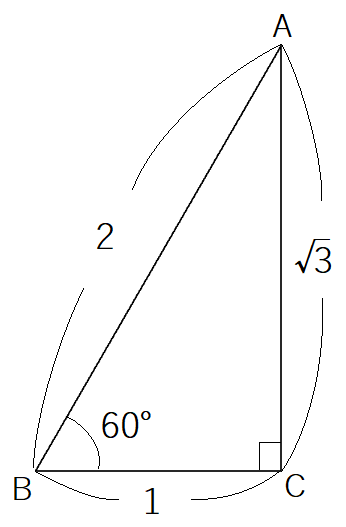
したがって角 は
とわかります。
一方 についても同様に考えると,
が先の
と相似なので
であり,したがって
とわかります。
例題2の解答
では,今度は に関する方程式を考えてみましょう。
例題3
次の についての方程式を解いてください。ただし
とします。
\begin{align}
\tan \theta = 1
\end{align}
冒頭で紹介した記事において
原点を中心とする半径 の円周上の点
について
は直線
の傾きだと表現しました。
すると,次の図のような角 を求めることになります。
候補が つあることに注意しましょう。
上の図の と
は次の
と相似です。
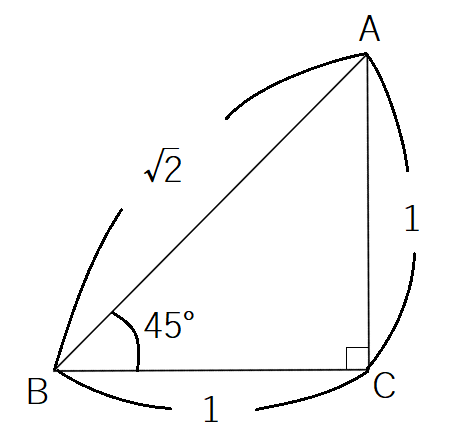
したがって,,
とわかります。
例題3の解答
では,例題1~3をもとにして,次の問題を解いてみましょう。
練習問題
次の についての方程式を解いてください。ただし
とします。
(1)
(2)
(3)
練習問題の解答
(1)
(2)
(3)