「相加平均と相乗平均の大小関係」の証明 2通り

証明したい内容は，次の通りです。

相加平均と相乗平均の大小関係

$a \gt 0，b \gt 0$ とします。このとき次の不等式が成り立ちます。

\begin{align}
\frac{a+b}{2} \geqq \sqrt{ab}
\end{align}

また等号成立条件，つまり $\displaystyle\frac{a+b}{2} = \sqrt{ab}$ となるのは $a=b$ のときです。

本記事では(2数のときの)相加平均と相乗平均の大小関係の証明を
2通り紹介します。

まずは，数式のみを使った単純な手法から。
$A \geqq B$ を示すために， $A-B \geqq 0$ を示します。

証明1

\begin{align}
(左辺)-(右辺)&=\frac{a+b}{2}-\sqrt{ab}\\
&=\frac{a+b}{2}-\frac{2\sqrt{ab}}{2}\\
&=\frac{a-2\sqrt{ab}+b}{2}\\
&=\frac{(\sqrt{a}-\sqrt{b})^2}{2} \geqq 0
\end{align}
となるので， $\displaystyle\frac{a+b}{2} \geqq \sqrt{ab}$ がいえます。

また等号が成立するのは， $\displaystyle\frac{(\sqrt{a}-\sqrt{b})^2}{2}=0$ となるときです。

\begin{align}
\frac{(\sqrt{a}-\sqrt{b})^2}{2}&=0\\
(\sqrt{a}-\sqrt{b})&=0\\
\sqrt{a}&=\sqrt{b}\\
a&=b
\end{align}

上の計算より， $a=b$ のとき，等号が成立します。

このように，不等式そのものと，等号が成り立つことを
基本的な式変形によって簡単に示すことができます。

次に，図形を用いた証明方法を紹介します。

証明2(図形を用いた証明)

次のような図を考えます。
点 $O$ を中心とする円があり，直径の両端を $A$ ， $B$ とします。
円周上の任意の位置に点 $P$ をとり，点 $P$ から線分 $AB$ への垂線と線分 $AB$ との交点を $H$ とします。
また，円周上に点 $C$ を $CO \perp AB$ となるようにとります。

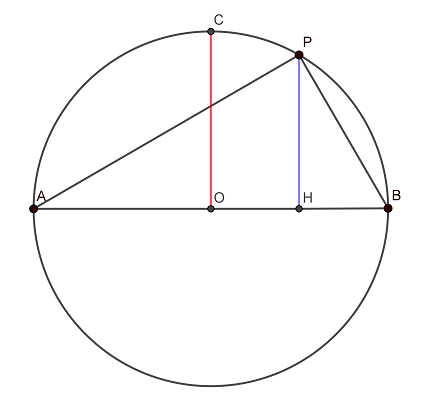
f:id:shibiremath:20210621020402p:plain

ここで $AH=a$ ， $BH=b$ とおくと， $CO=\displaystyle\frac{a+b}{2}$ ， $PH=\sqrt{ab}$ となります。
このことを説明します。

まず，線分 $CO$ は円の半径ですから，

$CO=\displaystyle\frac{a+b}{2} \tag{1}$
がいえます。これはちょうど2数 $a,b$ の相加平均です。

次に， $\bigtriangleup PAB$ について三平方の定理より

$AB^2 = PA^2 + PB^2 \tag{2}$
が成り立ちます。
更に $\bigtriangleup PAH$ と $\bigtriangleup PBH$ について，それぞれ三平方の定理より

$PA^2 = PH^2 + AH^2 \tag{3}$
$PB^2 = PH^2 + BH^2 \tag{4}$
が成り立ちます。
式(2)に式(3)，(4)を代入して

$AB^2=(PH^2 + AH^2) + (PH^2 + BH^2)$
を得ます。
$AB=a+b$ ， $AH=a$ ， $BH=b$ と $PH \gt 0$ に注意すればこの式は
\begin{align}
(a+b)^2 &= (PH^2 + a^2) + (PH^2 + b^2)\\
a^2 + 2ab + b^2 &= 2PH^2 + a^2 + b^2\\
2PH^2 &= 2ab\\
PH^2 &= ab\\
PH &= \sqrt{ab} \tag{5}
\end{align}
となります。これはちょうど2数 $a,b$ の相乗平均です。

さて，式(1)，(5)を比較します。
線分 $PH$ は線分 $CO$ より長くなることはありません。
したがって $CO \geqq PH$ ，すなわち $\displaystyle\frac{a+b}{2} \geqq \sqrt{ab}$ がいえます。

また $CO=PH$ となるのは点 $P$ が点 $C$ と重なるときで
このとき点 $H$ は点 $O$ と重なりますから $AH=BH$ となります。
言いかえれば， $\displaystyle\frac{a+b}{2} = \sqrt{ab}$ が成り立つのは $a=b$ のとき
となります。