特定の角の三角比（30°，45°，60°など）

本記事を読む前に，こちらの記事も合わせて読んでおくことをおすすめします。

shibiremath.hatenablog.com

はじめに
45°の三角比
30°，60°の三角比
30°，45°，60°以外の三角比
おわりに

はじめに

三角比 $\sin \theta , \cos \theta , \tan \theta$ について，角度によっては
比較的簡単な形でその値を求められるものがあります。
とくに， $30^{\circ} , 45^{\circ} , 60^{\circ}$ の三角比は非常に有名で
これらを知っていることが前提で問題を出されることがほとんどです。

では早速考えてみましょう。まずは $45^{\circ}$ の三角比です。

45°の三角比

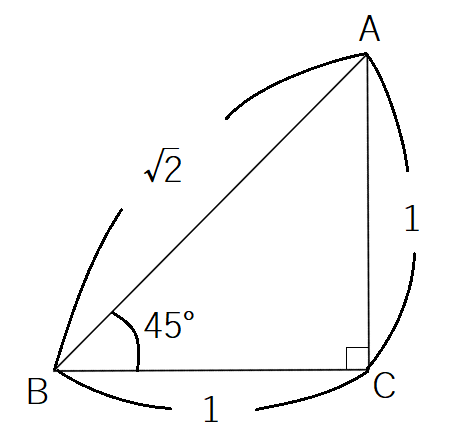
次のような直角三角形 $ABC$ を考えます。

三角形の内角の和は $180^{\circ}$ ですから，これは二等辺三角形です。
等しい $2$ 辺(この図では $辺AC , BC$ )の長さを $1$ とおくと
三平方の定理より
\begin{align}
AB^2 &= AC^2 + BC^2\\
AB^2 &= 1^2 + 1^2\\
AB^2 &= 2\\
(AB & \gt 0 なので)\\
AB &= \sqrt{2}
\end{align}
となります。したがって
$\sin 45^{\circ} = \displaystyle\frac{1}{\sqrt{2}},\cos 45^{\circ} = \displaystyle\frac{1}{\sqrt{2}},\tan 45^{\circ} = 1$
であることがわかります。

30°，60°の三角比

次は $30^{\circ}$ の三角比です。
下の図のような直角三角形 $ABC$ を考えます。

三角形の内角の性質から $\angle A = 60^{\circ}$ はすぐにわかりますが
$45^{\circ}$ のときほど簡単にはわかりません。
そこで次のように工夫してやりましょう。
三角形 $ABC$ と合同な三角形を，辺 $BC$ を合わせるように描きます。

すると，上の図の三角形 $BAA'$ は正三角形になります。
また三角形 $ABC$ と三角形 $A'BC$ が合同である前提から
$AC = CA' = \displaystyle\frac{1}{2} BA$ とわかります。
そこで $BA = 2 , AC = 1$ とします。
三角形 $ABC$ において三平方の定理より
\begin{align}
AB^2 &= AC^2 + BC^2\\
2^2 &= 1^2 + BC^2\\
BC^2 &= 3\\
(BC & \gt 0 なので)\\
BC &= \sqrt{3}
\end{align}
となります。
したがって， $\sin 30^{\circ} = \displaystyle\frac{1}{2} , \cos 30^{\circ} = \displaystyle\frac{\sqrt{3}}{2} , \tan 30^{\circ} = \displaystyle\frac{1}{\sqrt{3}}$
であることがわかります。

では， $60^{\circ}$ の三角比もすぐにわかりますね。

例題1

$\sin 60^{\circ} , \cos 60^{\circ} ,\tan 60^{\circ}$ の値をそれぞれ求めてください。

例題1の解答

$\sin 60^{\circ}=\displaystyle\frac{\sqrt{3}}{2} , \cos 60^{\circ}=\displaystyle\frac{1}2{} ,\tan 60^{\circ}=\sqrt{3}$ です。

さっき登場した $30^{\circ}$ の角を持つ直角三角形の向きを変えればすぐにわかります。

　　　→向きを変える→　　　

30°，45°，60°以外の三角比

ところで，三角比の値を具体的に求めることができるのは
$30^{\circ} , 45^{\circ} , 60^{\circ}$ のときだけなのでしょうか？

いいえ，そういうわけではありません。
これら以外にも比較的簡単な形で
三角比の値を求めることができる角度はあります。

例えば，次の問題はどうでしょう。

例題2

次の図を参考にして， $\sin 15^{\circ} , \cos 15^{\circ} , \tan 15^{\circ}$ の値を求めてください。
(もしも値を求める最中に二重根号(根号 $\sqrt{}$ の中にまた根号がある表記)が現れたとき，処理の方法がわからなければとくに気にせずそのまま突き進んでください)

例題2の解答と解説

まず $\triangle ACD$ は $30^{\circ}$ の角を持つ直角三角形ですから
$AC=2 , CD=\sqrt{3}$ がすぐにわかります。
次に $\angle ACB = 150^{\circ}$ で， $\triangle ABC$ に着目すると
三角形の内角の和の性質から $\angle BAC=15^{\circ}$ とわかります。
つまり $\triangle ABC$ は $AC=BC$ の二等辺三角形です。
したがって $BC=AC=2$ ですから $BC=2+\sqrt{3}$ とわかります。
ここで $\triangle ABD$ に注目すると
$\tan 15^{\circ} = \displaystyle\frac{1}{2+\sqrt{3}} = 2-\sqrt{3}$ が求められました。

さて， $\triangle ABD$ について辺 $AB$ 以外の2辺は既にわかっていますから
三平方の定理から $AB$ の長さを計算しましょう。
\begin{align}
AB^2 &= AD^2 + BD^2\\
AB^2 &= 1^2 + (2+\sqrt{3})^2\\
AB^2 &= 1+ 4 + 4\sqrt{3} + 3\\
AB^2 &= 8 + 4 \sqrt{3}\\
(AB & \gt 0 なので)\\
AB &= \sqrt{8+4 \sqrt{3}}
\end{align}
$AB$ の値を求められましたが，二重根号になってしまいました。
今回の形なら二重根号は避けることができて
\begin{align}
AB &= \sqrt{8+4 \sqrt{3}}\\
&= \sqrt{8+2 \sqrt{12}}\\
&= \sqrt{(\sqrt{6} + \sqrt{2})^2}\\
&= \sqrt{6} + \sqrt{2}
\end{align}
となります。

そういうわけで，もう一度 $\triangle ABD$ に注目すれば
$\sin 15^{\circ} = \displaystyle\frac{1}{\sqrt{6} + \sqrt{2}} = \displaystyle\frac{\sqrt{6} - \sqrt{2}}{4}$

$\cos 15^{\circ} = \displaystyle\frac{2 + \sqrt{3}}{\sqrt{6} + \sqrt{2}} = \displaystyle\frac{(2 + \sqrt{3})(\sqrt{6} - \sqrt{2})}{4} = \displaystyle\frac{\sqrt{6} + \sqrt{2}}{4}$